Apa itu Teorema Pythagoras?
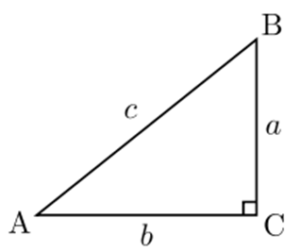
Apa itu teorema Pythagoras? Teorema Pythagoras adalah suatu pernyataan mengenai relasi atau hubungan sisi-sisi dalam suatu segitiga siku-siku. Misalkan kita diberikan sebuah segitiga siku-siku sebagai berikut:
"Teorema Pythagoras mengatakan bahwa dalam suatu segitiga siku-siku, jumlah kuadrat dari sisi-sisi yang saling tegak lurus sama dengan kuadrat dari sisi miringnya."
Secara matematis, kita bisa bilang bahwa untuk segitiga siku-siku seperti pada gambar diatas, persamaan ini berlaku:
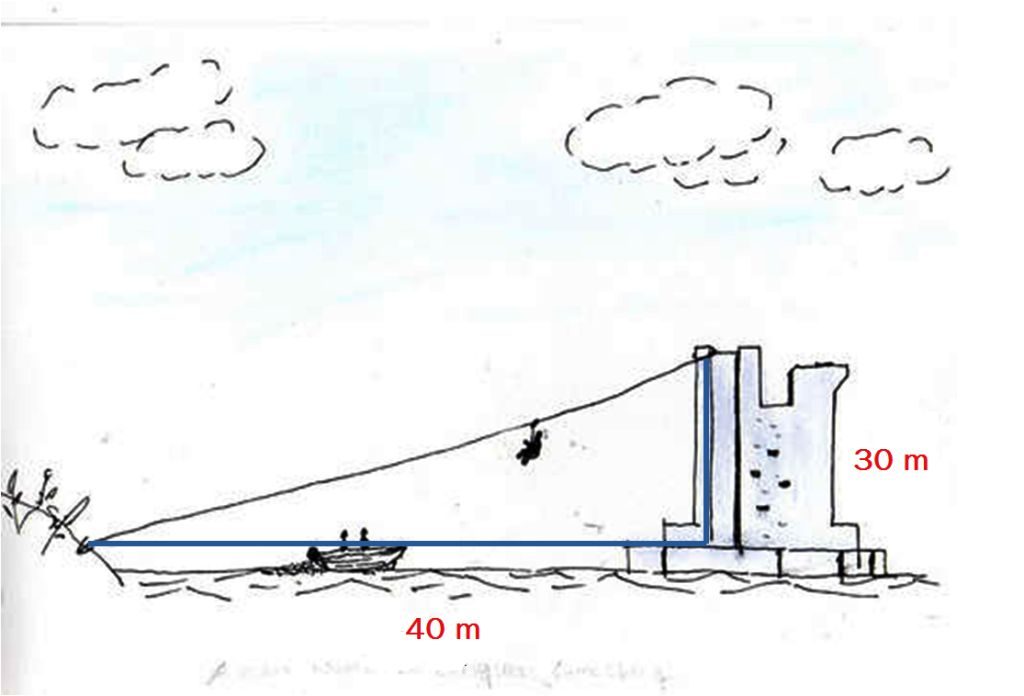
Kita masuk ke contoh sederhana. Misalkan, pak Made ingin membuat wahana flying fox seperti skema segitiga siku-siku yang terlihat di bawah ini.
Tinggi menara adalah 30 m. Jarak dari menara ke dataran seberang adalah 40 m. Berapakah panjang tali yang diperlukan pak Made untuk dipasang dari atas menara, menyusuri perairan ke dataran seberang? Walah, gampanglah soal ini buat lu.
Misalkan  adalah tinggi menara,
adalah tinggi menara,  adalah jarak antara menara dan dataran di seberangnya, dan
adalah jarak antara menara dan dataran di seberangnya, dan  adalah panjang tali flying fox yang diperlukan. Dengan teorema Pythagoras, kita dapat:
adalah panjang tali flying fox yang diperlukan. Dengan teorema Pythagoras, kita dapat:
Karena panjang selalu bernilai positif, kita ambil  . Jadi, panjang tali yang diperlukan pak Made adalah 50 m.
. Jadi, panjang tali yang diperlukan pak Made adalah 50 m.
Keliatannya simple kan? Tapi perhitungan jarak pada hubungan sisi-sisi segitiga ini pastinya banyak kita temukan di berbagai aspek kehidupan. Oleh karenanya, Teorema Pythagoras menjadi fondasi trigonometri. Teorema Pythagoras menjadi dasar perhitungan buat teorema-teorema lain di matematika, khususnya trigonometri. Dan tanpa trigonometri, kita tidak akan punya banyak hal yang membentuk peradaban manusia sekarang. Tanpa trigonometri, tidak akan ada sains, arsitektur, ilmu kelautan, astronomi, bahkan ga akan ada rumah, mobil, komputer, dan berbagai teknologi modern yang kita nikmati sekarang.
Pembuktian Teorema Pythagoras Modern
Nah, sekarang kalian udah tau kenapa Teorema ini dinamakan Pythagoras. Kita bisa lanjut bahas perkembangan teorema ini. Seperti yang disebut di atas, teorema Pythagoras  yang sering kita pakai sekarang, berbeda dengan perhitungan ketika digunakan oleh orang-orang di peradaban kuno atau ketika Pythagoras berhasil membuktikannya. Tapi biar kalian bisa melihat kontrasnya, sebaiknya kita mulai dulu dengan membuktikan Teorema Pythagoras versi modern.
yang sering kita pakai sekarang, berbeda dengan perhitungan ketika digunakan oleh orang-orang di peradaban kuno atau ketika Pythagoras berhasil membuktikannya. Tapi biar kalian bisa melihat kontrasnya, sebaiknya kita mulai dulu dengan membuktikan Teorema Pythagoras versi modern.
Misalkan kita punya gambar seperti berikut:
Maksud dari gambar ini adalah kita diberikan empat segitiga siku-siku yang identik, di mana keempat segitiga siku-siku tersebut disusun sedemikian rupa sehingga membentuk suatu persegi besar dengan sisi  dan sebuah persegi putih dengan sisi
dan sebuah persegi putih dengan sisi  di dalam persegi besar tersebut.
di dalam persegi besar tersebut.
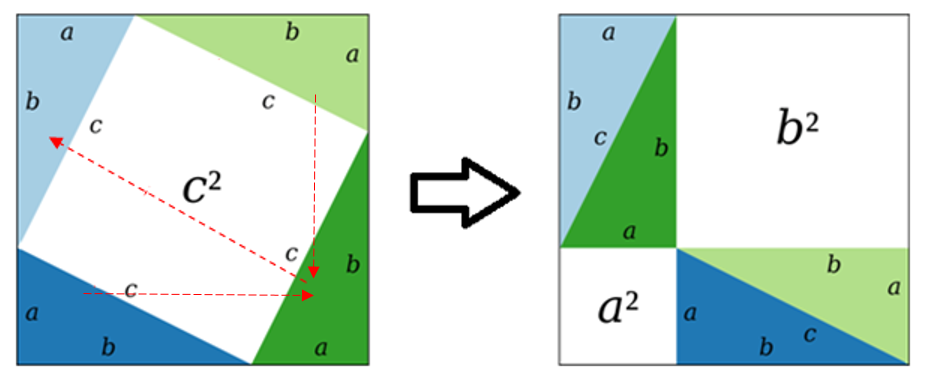
Sekarang, kita ingin mengatur letak segitiga siku-sikunya sedemikian rupa sehingga kita mendapatkan dua buah persegi dengan sisi-sisi  dan sisi-sisi
dan sisi-sisi  . Caranya adalah, kita geser segitiga siku-siku berwarna hijau tua dari kanan bawah ke kiri atas sehingga dia menempel segitiga siku-siku berwarna biru muda. Kemudian, kita geser pula segitiga siku-siku berwarna biru tua dari kiri ke kanan dan segitiga siku-siku berwarna hijau muda dari atas ke bawah sedemikian rupa sehingga keduanya saling menempel. Dari proses tersebut, kita mendapatkan gambar sebagai berikut:
. Caranya adalah, kita geser segitiga siku-siku berwarna hijau tua dari kanan bawah ke kiri atas sehingga dia menempel segitiga siku-siku berwarna biru muda. Kemudian, kita geser pula segitiga siku-siku berwarna biru tua dari kiri ke kanan dan segitiga siku-siku berwarna hijau muda dari atas ke bawah sedemikian rupa sehingga keduanya saling menempel. Dari proses tersebut, kita mendapatkan gambar sebagai berikut:
Supaya melihatnya lebih enak, coba kita bandingkan kedua gambar persegi di atas menjadi seperti ini:
Dari gambar gabungan kedua persegi diatas, terlihat bahwa kita hanya menggeser segitiga siku-siku berwarna biru tua, hijau tua, dan hijau muda. Itu berarti, luas persegi luar dengan sisi  baik sebelum maupun sesudah pergeseran segitiga siku-siku adalah sama besar. Secara matematis, kita bisa bilang bahwa:
baik sebelum maupun sesudah pergeseran segitiga siku-siku adalah sama besar. Secara matematis, kita bisa bilang bahwa:
Kurangkan kedua ruas persamaan di atas dengan  , kita dapat:
, kita dapat:

Pembuktian yang kita lakukan di atas sebenarnya berasal dari gagasan Pythagoras sendiri. Pembuktiannya sangat sederhana dan elegan ya.
Teorema Awal Pythagoras
Sampai di sini, berharapnya sih kalian udah ngerti dengan pembuktian Teorema Pythagoras modern. Sekarang kalian udah bisa masuk dan melihat kontrasnya dengan Teorema Pythagoras versi awal. Pada versi modern, kita biasanya menafsirkan teorema Pythagoras sebagai relasi antar PANJANG dari sisi-sisi segitiga siku-siku. Namun, interpretasi teorema Pythagoras yang sekarang ini sebenarnya agak berbeda dengan interpretasi teorema Pythagoras oleh Pythagoras sendiri semasa dia hidup.
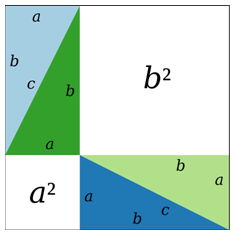
Pythagoras menafsirkan teorema ini sebagai relasi antar LUAS PERSEGI atau bujur sangkar yang terbentuk di setiap sisi-sisi segitiga siku-siku. Gambarnya kira-kira seperti ini:
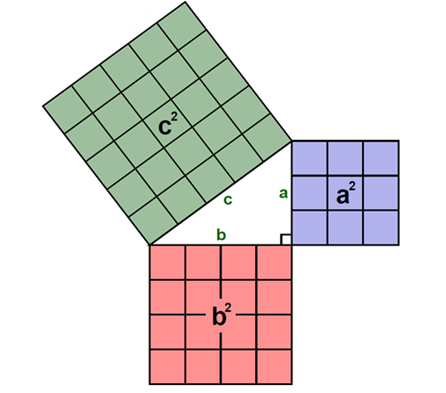
Jadi, pernyataan teorema Pythagoras berdasarkan interpretasi Pythagoras adalah sebagai berikut:
"Dalam suatu segitiga siku-siku, jumlah luas dari masing-masing persegi yang terbentuk dari sisi-sisi yang saling tegak lurus sama dengan luas dari persegi yang terbentuk dari sisi miringnya"
Dari sini aja udah keliatan banget bedanya. Secara matematis, dalam suatu segitiga siku-siku seperti gambar yang kedua, persamaan ini berlaku:
di mana:
Pernyataan matematis ini pertama kali dinyatakan oleh Euclid, seorang matematikawan Yunani kuno yang terkenal dengan bukunya berjudul The Elements.
Jadi, matematikawan zaman Yunani kuno, seperti Euclid, tidak melihat teorema Pythagoras ini sebagai relasi antar panjang dari setiap sisi-sisi segitiga siku-siku, tetapi sebagai relasi antar luas dari persegi yang terbentuk di setiap sisi-sisi segitiga siku-siku.
Mengapa bisa demikian? Karena jika teorema tersebut dinyatakan dalam relasi antara antar panjang setiap sisi-sisi segitiga siku-siku, maka Pythagoras harus berurusan dengan bilangan irasional. Apa itu bilangan irasional? Semua bilangan yang bisa dinyatakan dengan bentuk pecahan bilangan bulat seperti  ,
,  , dan sebagainya adalah bilangan rasional. Bilangan real yang tidak bisa dinyatakan dalam bentuk pecahan seperti itu adalah bilangan irasional. Jadi, kalau Pythagoras menemukan suatu segitiga yang masing-masing sisinya adalah 1 dan 2 misalnya, maka berapa panjang sisi miringnya?
, dan sebagainya adalah bilangan rasional. Bilangan real yang tidak bisa dinyatakan dalam bentuk pecahan seperti itu adalah bilangan irasional. Jadi, kalau Pythagoras menemukan suatu segitiga yang masing-masing sisinya adalah 1 dan 2 misalnya, maka berapa panjang sisi miringnya?
Nah, itu adalah bilangan irasional. Jangankan alat bantu hitung seperti kalkulator, simbol akar kuadrat aja belum ada pada jaman itu. Simbol akar kuadrat pertama kali diperkenalkan oleh Christoph Rudolff pada tahun 1525 (2000 tahun lebih setelah Pythagoras lahir). Jadi, Pythagoras hanya bisa menafsirkan kuantitas bilangan irasional seperti  dalam geometri saja, yaitu sebagai segmen garis yang terbentuk dari segitiga siku-siku sama kaki. Doi ga tau nilai sesungguhnya dari
dalam geometri saja, yaitu sebagai segmen garis yang terbentuk dari segitiga siku-siku sama kaki. Doi ga tau nilai sesungguhnya dari  .
.
Gimana Teorema Pythagoras Berkembang Seperti Sekarang?
Trus netizen pun bertanya:
Kok bisa teorema Pythagoras versi awal yang menggunakan relasi antar luas persegi berubah menjadi versi modern yang mengunakan relasi antar panjang dalam segitiga siku-siku?
Jawabannya adalah peristiwa yang dikenal sebagai “Dilema Akar 2” yang diduga ditemukan oleh seseorang bernama Hippasus, salah satu pengikut Pythagoras. Pada tahun sekitar 500 Sebelum Masehi, dia berhasil menunjukkan bahwa:
"tidak ada bilangan rasional yang jika dikuadratkan, maka hasilnya sama dengan dua"
Ingat, pada zaman itu, para matematikawan belum mengenal konsep bilangan irasional, mereka cuma taunya bilangan rasional aja. Dia menemukan hal ini ketika dia menerapkan teorema Pythagoras untuk mencari rasio antara sisi miring dan sisi alas dari suatu segitiga siku-siku sama kaki. Ketika dia berusaha melakukan hal ini, dia menemukan bahwa mustahil untuk menyatakan kuadrat dari rasio antara sisi miring dan sisi alas dari suatu segitiga siku-siku sama kaki yang hasilnya sama dengan 2.
Maksudnya apa sih? Coba deh kita jabarkan secara matematis:.
Kita punya premis: Tidak ada bilangan rasional  yang memenuhi
yang memenuhi
Gimana cara buktiinnya?
- Asumsikan bahwa
dan
adalah bilangan bulat (bilangan negatif, positif, atau nol), di mana
.
- Trus, asumsikan juga bahwa
dan
TIDAK memiliki faktor persekutuan atau kelipatan yang sama supaya pecahan
merupakan pecahan dalam bentuk yang paling sederhana untuk memenuhi persamaan di atas. Jika
dan
memiliki faktor persekutuan, kita bisa membagi
dan
dengan faktor persekutuan tersebut sehingga pecahan
menjadi pecahan dalam bentuk yang paling sederhana. Kalo misalnya
dan
, mereka punya faktor persekutuan dong,
. Nah, ini ga boleh ya. Jadi
dan
ga boleh memiliki faktor persekutuan/kelipatan untuk bisa memenuhi premis di atas.
- Oke lanjut. Dengan manipulasi aljabar, kita dapat:
- Nah, dari baris terakhir kita tau kalo
pasti bilangan genap. Kenapa? Kan
sama dengan hasil dari 2 dikali
. Apapun bilangannya, kalo dikali 2 pasti jadi genap dong.
- Karena
adalah bilangan genap (bilangan yang habis dibagi dua), maka
harus berupa bilangan genap juga. Ya ga? Suatu bilangan ganjil kalo dikuadratkan, ga mungkin menghasilkan bilangan genap, pasti ganjil juga. Contohnya, 3 adalah bilangan ganjil karena 3 tidak habis dibagi 2. Kuadrat dari 3 adalah 9, di mana 9 juga merupakan bilangan ganjil karena tidak habis dibagi 2. Jadi, untuk menghasilkan bilangan kuadrat yang genap,
harus berupa bilangan genap juga.
- Karena
bilangan genap, kita bisa buat
.
- Substitusikan
ke persamaan
, kita dapat:
- Di sini, terlihat kalo
juga merupakan bilangan genap.
- Dengan alasan yang sama seperti dijelaskan di atas, kita simpulkan bahwa
juga merupakan bilangan genap, katakanlah
.
- Karena
dan
, terlihat bahwa
dan
memiliki faktor persekutuan, yaitu 2.
- Ini bertentangan dengan asumsi di awal bahwa
dan
tidak memiliki faktor persekutuan. Artinya, asumsi bahwa ada suatu pecahan
dalam bentuk yang paling sederhana yang memenuhi
adalah salah.
- Kesimpulannya, tidak ada bilangan rasional
yang memenuhi persamaan
.
- Terbukti!
Penemuan Hippasus ini ternyata sangat mengejutkan pengikut Pythagoras karena ini bertentangan dengan apa yang mereka yakini selama ini, yaitu segalanya bisa dinyatakan dalam rasio antar dua bilangan asli. Menurut legenda, karena penemuan Hippasus ini, dia bahkan ditenggelamkan ke laut oleh para pengikut Pythagoras. Penemuan Hippasus ini jugalah yang mengawali munculnya konsep bilangan irasional sehingga mengakibatkan perubahan pernyataan teorema Pythagoras menjadi teorema Pythagoras seperti yang kita kenal sekarang ini.
Soo, that's it yang bisa ku bagi ke kalian. Untuk sharing dan segala macamnya ku tunggu di kolom komentar. See u next!

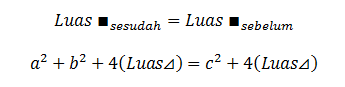








0 comments:
Post a Comment